 Index
> Windows > how do x^6 on sse or avx ?
Index
> Windows > how do x^6 on sse or avx ? |
| Author |
|
|
revolution 16 Oct 2025, 23:42
A power of 6 can be done with three multiplies.
a = x*x ; x^2 b = a*x ; x^3 c = b*b ; x^6 |
|||
|
|
Roman 17 Oct 2025, 00:08
Sorry my mistake.
Code: ;x^8 align 32 x dd 1f,2f,3f,4f,5f,6f,7f,8f vmovaps ymm0,yword [x] vmulps ymm0, ymm0, ymm0 ; x^2 vmulps ymm0, ymm0, ymm0 ; x^4 vmulps ymm0, ymm0, ymm0 ; x^8 ;after in ymm0 1f^8 ,2f^8 ,3f^8 ,4f^8 ,5f^8 ,6f^8 ,7f^8 ,8f^8 Code: x dd 3.0 movss xmm1,[x] movss xmm0,xmm1 mulss xmm0,xmm0 ;x^2 mulss xmm0,xmm0 ;x^4 mulss xmm1,xmm0 ;x^5 xmm1=3^5=243 |
|||
|
|
revolution 17 Oct 2025, 06:30
In general x-to-power-of-n can be computed in no more than [ bsr(n) + popcnt(n) - 1 ] multiplies.
|
|||
|
|
Roman 17 Oct 2025, 14:37
Quote:
Very interesting see example how do this. |
|||
|
|
Tomasz Grysztar 17 Oct 2025, 17:14
Roman wrote:
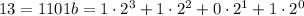
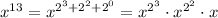
So if we have the square powers of x ready, we only need to perform 2 more multiplications - this is the "popcnt(n) - 1" portion of revolution's formula. Now, taking into consideration that 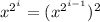 it follows that we can compute it follows that we can compute 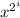 by squaring i times, and we get all the intermediate squares on the way. This is the "bsr(n)" part of the formula. by squaring i times, and we get all the intermediate squares on the way. This is the "bsr(n)" part of the formula.
For n = 13 we get this sequence of multiplications: a = x*x b = a*a c = b*b x^13 = c*b*x For final calculation you take the product of all the consecutive squares and remove the ones that correspond to zeros in the binary representation of n. Here, because 13 = 1101b, it meant removing "a" from "c*b*a*x" (as "a" corresponds to the only zero in 1101b). |
|||
|
|
Roman 18 Oct 2025, 08:13
Quote:
I thinked this code help do two multiplication. But if not, this code only confusing and complicating. But not help. |
|||
|
< Last Thread | Next Thread > |
Forum Rules:
|

